[ 백준 ] 11729번 - 하노이 탑 이동 순서 (Python)

기본 정보

• Level: silver 1
• Problem Link: 하노이 탑 이동 순서
• Problem Number: 11729
• My Solution Link: 나의 풀이
• Algorithm I used: 분할정복(divide & conquer)

문제

• 하노이 탑 옮기는 규칙
  • 한 번에 한 개의 원판만 옮길 수 있다.
  • 항상 위의 것이 아래 것보다 작아야 한다.
• 최소 이동 횟수, 그 때의 이동 순서

알고리즘

• 하노이 탑 3단계

  

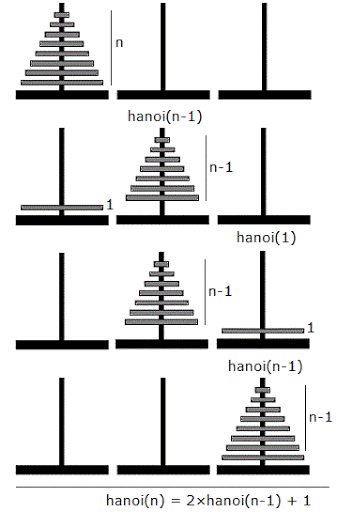
  1. 가장 큰 원반 제외한 원반들을 두 번째 막대로 옮긴다.
  2. 가장 큰 원반을 세 번째 막대로 옮긴다.
  3. 두 번째 막대에 있던 작은 원반들을 세 번째 막대로 옮긴다.

• $N$개의 원판 → 최소 $2^N-1$번 소요

  4개의 원판

  1. hanoi(3)을 2번 기둥으로 옮긴다.
  2. 가장 큰 원판을 3번 기둥으로 옮긴다.
  3. 2번 기둥에 있던 hanoi(3)을 3번 기둥으로 옮긴다.

  → hanoi(3)을 두 번 옮기고 큰 원판 한 번 옮기기

나의 시도

• 하노이 탑 문제를 처음 풀어보기 때문에 감이 잡히지 않아 구글링으로 알고리즘을 공부했다. (어려워…😢)

def hanoi(n, start, via, to):
    """
    args
        param n : 원판 개수
        param start : 원래 위치 (막대 번호)
        param via : start에서 to로 가기 위한 경유지 (막대 번호)
        param to : 옮겨갈 위치 (막대 번호)
    상황
        start에서 to로 via를 거쳐 총 n개의 원반을 운반
    """

    if n == 1:
        print(f'{start} {to}')
    else:
        hanoi(n-1, start, to, via)  # 나머지 원판들 묶음이 두 번째 막대로 옮겨진다.
        print(f'{start} {to}')  # 가장 큰 원판이 세 번째 막대로 옮겨진다.
        hanoi(n-1, via, start, to)  # 나머지 원판들 묶음이 세 번째 막대로 옮겨진다.

N = int(input())
print(2**N - 1)
hanoi(N,1,2,3)