[ 데이터구조 ] Binary Search

이진탐색 (이분탐색)

주어진 문제

• 서로 다른 n개의 정렬된 수가 list에 저장되어 있을 때, 특정한 값을 찾아라

필요한 변수

• left : 범위 중 가장 왼쪽 원소의 index
• right : 범위 중 가장 오른쪽 원소의 index
• middle : (left+right)/2 → 버림해야 함.

알고리즘

while left <= right:
	middle = (left + right) / 2

	if (찾는 수) < (middle이 가리키는 수):
		right = middle - 1

	elif (찾는 수) == (middle이 가리키는 수):
		return middle

	else:  # 찾는 수 > middle이 가리키는 수
		left = middle + 1

• 예시

  

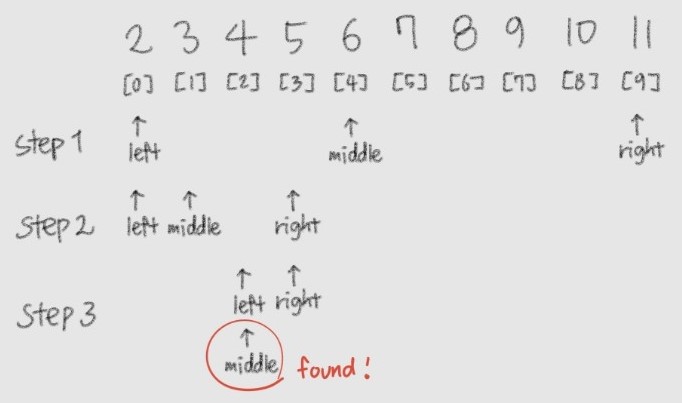
• 시간복잡도 : $O(logN)$

재귀적 구현

def BinarySearchRecursive(array, searchNum, left, right):
    middle = (left + right) // 2

    while array[left] <= array[right]:
        if array[middle] > searchNum:
            return BinarySearchRecursive(array, searchNum, left, middle-1)
        elif array[middle] < searchNum:
            return BinarySearchRecursive(array, searchNum, middle+1, right)
        else:
            return middle

    return False

# 원소의 개수, 원하는 수
n, searchNum = map(int,input().split())

nums = [elem for elem in map(int,input().split())]

# 초기 설정
left, right = 0, n-1

result = BinarySearchRecursive(nums,searchNum,left,right)

if not result:
    print("원소가 존재하지 않습니다.")
else:
    print(result)

반복문 구현

def BinarySearchIterative(array, searchNum, left, right):
    while left <= right:
        middle = (left + right) // 2

        if array[middle] > searchNum:
            right = middle -1
            continue
        elif array[middle] < searchNum:
            left = middle + 1
            continue
        else:
            return middle
    return False

# 원소의 개수, 원하는 수
n, searchNum = map(int,input().split())

nums = [elem for elem in map(int,input().split())]

# 초기 설정
left, right = 0, n-1

result = BinarySearchIterative(nums,searchNum,left,right)

if not result:
    print("원소가 존재하지 않습니다.")
else:
    print(result)

파이썬 bisect 모듈

• 이진탐색을 구현한 모듈

모듈 내 대표적인 메소드

오름차순으로 정렬된 리스트에 새로운 수를 삽입하려 할 때…

• bisect_left(literable, value)
  • 어떠한 수의 왼쪽으로 삽입
  • 동일한 수가 이미 리스트에 존재한다면 → 기존 항목의 왼쪽
• bisect_right(literable, value)
  • 어떠한 수의 오른쪽으로 삽입
  • 동일한 수가 이미 리스트에 존재한다면 → 기존 항목의 오른쪽

두 메소드 모두 새로 들어갈 수의 index를 반환한다.

사용예시

from bisect import bisect_left, bisect_right

nums = [0,1,2,3,4,5,6,7,8,9] 
n = 5 # 삽입할 수 

bisect_left(nums, n) # 좌측에 삽입한다. 결과: 5
bisect_right(nums, n) # 우측에 삽입한다. 결과: 6

Parametric Search

• 최적화 문제를 결정 문제(Yes/No)로 바꾸어 해결하는 기법
  • 특정한 조건을 만족하는 가장 알맞은 값을 빠르게 찾는 문제를 풀 때, 탐색 범위를 좁혀가며 각 범위 내에서 조건 만족 여부를 확인하는 방식으로 값을 찾는다.
• 이 문제는 이진 탐색을 이용하여 해결할 수 있다.