[ 데이터구조 ] Graph

그래프 (Graph)

• node + edge로 구성된 자료구조
• Tree? directed acyclic graph! (DAG)

그래프 용어

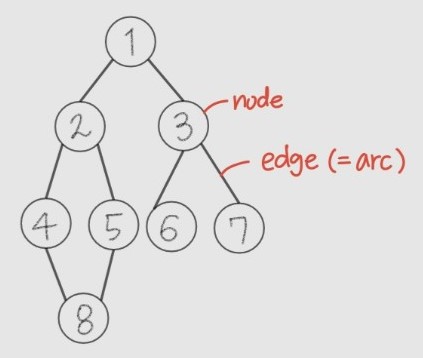
• cycle : node가 edge를 통해 다시 본인 node로 돌아오는 것 (현재 node를 제외하고 중복 X)
• 노드의 degree : branch 개수
• directed graph vs. undirected graph
• 특정 두 node간의 edge를 수식적으로 표현하면…
  • undirected graph라면 ($v_0$,$v_1$)
  • directed graph라면 <$v_j$,$v_k$>

인접 행렬, 인접 리스트

• 인접 행렬 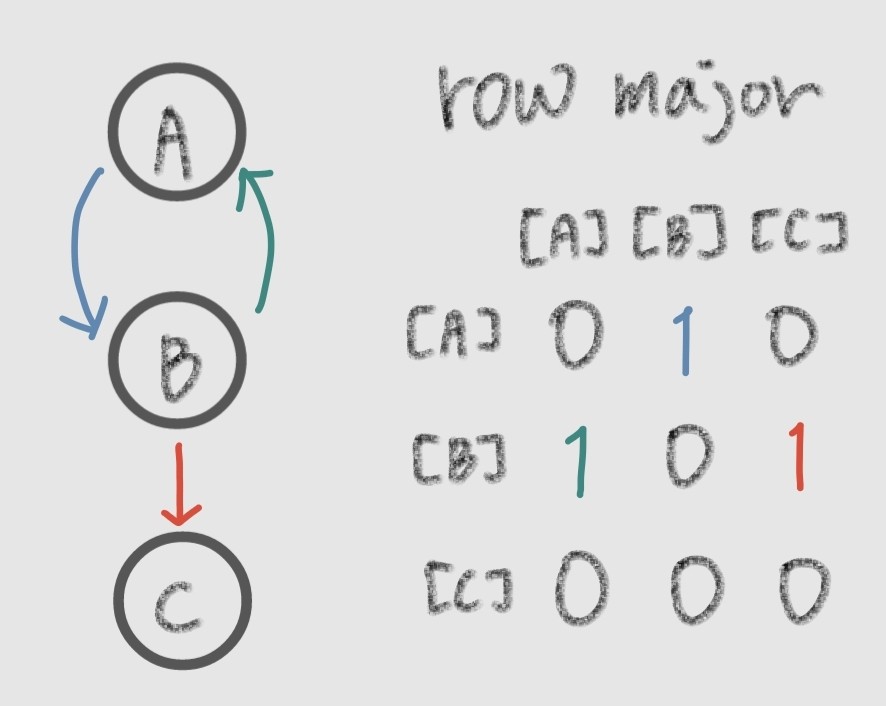n개의 node를 가지는 그래프에 대해 n*n 인 2차원 배열로 표현

• 인접 리스트 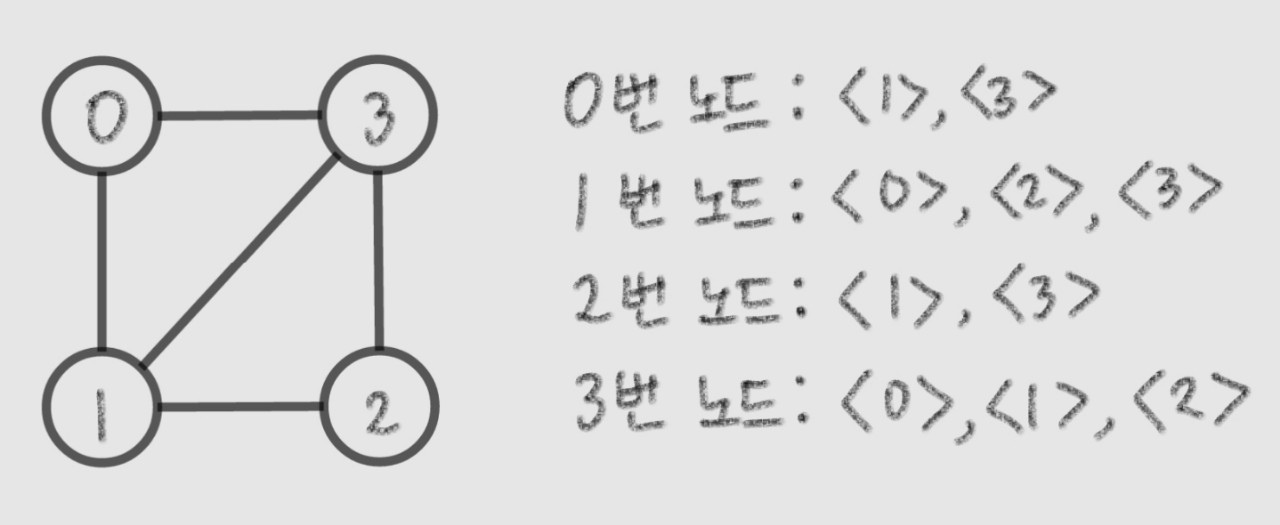n개의 정점 각각에 대해 인접한 정점들을 표현한 리스트

연결 그래프 (connected graph)

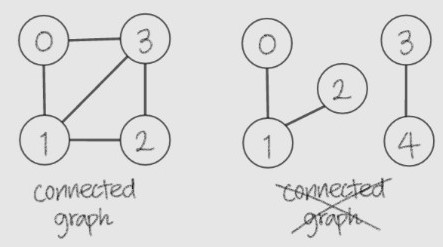
• 서로 다른 모든 쌍의 node들 사이에 경로가 있는 undirected graph
  • 좌측) 0→1, 0→2, 0→3, 1→2, 1→3, 2→3 모두 가는 경로가 있다.
  • 우측) 2→3 혹은 3→2로 갈 수 있는 경로가 없다.
• 연결요소 : 최대 연결 부분 그래프 e.g.) 위 사진의 오른쪽 그래프는 {0,1,2},{3,4}로 2개의 연결 요소를 갖는다.

강력 연결 vs. 약한 연결

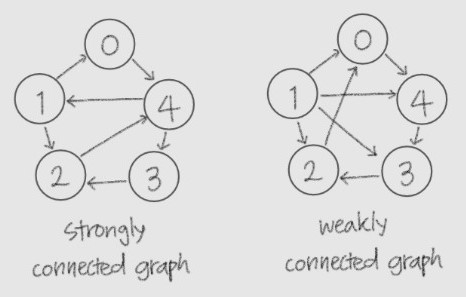
• 강력 연결 (strongly connected) 서로 다른 모든 노드쌍 u,v에 대해 u→v,v→u 양쪽으로 경로 존재 (쌍방향)
  • 강력 연결 요소 : 강력 연결된 최대 subgraph
• 약한 연결 (weakly connected) 서로 다른 모든 노드쌍 u,v에 대해 u→v 혹은 v→u 한쪽으로만 경로 존재 (단방향)

최단경로

신장 트리 (spanning Tree)

• 연결 그래프의 부분 그래프
• 연결 그래프의 모든 node와 일부 edge으로 구성된 트리
• DFS, BFS에서 사용한 edge 집합이 결국 spanning tree!
• 최소연결 부분 그래프 (min. connected subgraph)

최단거리

• 기본적으로 spanning tree를 만드는 것이다.
  1. Dijkstra [다익스트라] algorithm → 시간 좀 걸리는 방법
  • 이전까지의 최단 정보 거리를 고려하여 최단 거리 구하는 알고리즘
  • 동작방법
    ① 아직 방문하지 않았던 정점 中 거리가 가장 짧은 점점 방문
    ② 해당 정점에서 인접하고 방문하지 않은 점점들의 거리 갱신

1. Kruskal MST(min. spanning tree) algo.
   • Greedy 하게 MST 구하는 알고리즘
   • 동작방법
     ① 그래프의 간선들 → 가중치 오름차순 정렬
     ② ① 에서 순서대로 (즉, 작은것부터) cycle 을 형성하지 않게 하는 간선 선택
     ③ 해당간선을 현재 MST 집합에 추가
     ④ ②~③ 반복하다 ‘정점 개수 - 1’개의 간선을 선택했다면 종료