[ 데이터구조 ] Heap

tree에서 이어지는 내용입니다.

• 이전 포스팅 보러가기 : 트리

힙 (Heap)

max heap

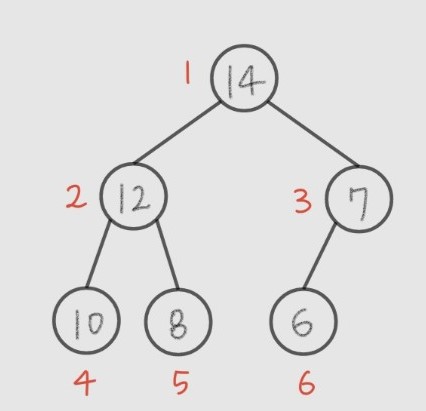
• complete binary tree이다.
• 노드의 값들이 중복 가능하다.
• 현재 노드에 있는 값이 직계후손의 값들보다 크거나 같다.

min heap

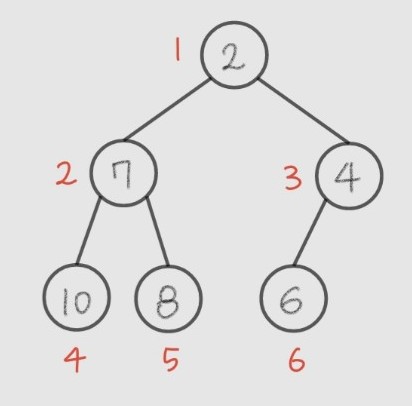
• complete binary tree이다.
• 노드의 값들이 중복 가능하다.
• 현재 노드에 있는 값이 직계후손의 값들보다 작거나 같다.

삽입 (max heap 기준)

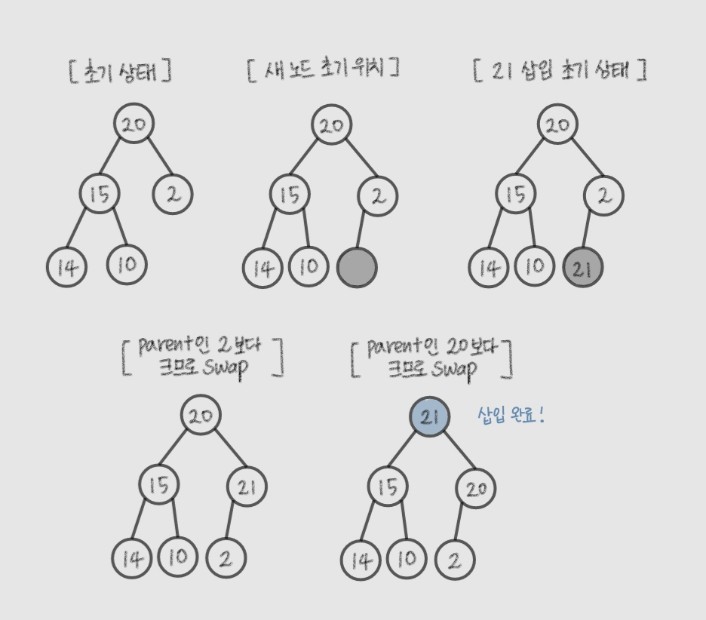
• 삽입 위치 : complete binary tree 순서 상 그 다음 위치
• 동작 : 초기 삽입 위치로부터 parent 쪽으로 옳은 위치를 찾아 계속 올라간다.

삭제 (max heap 기준)

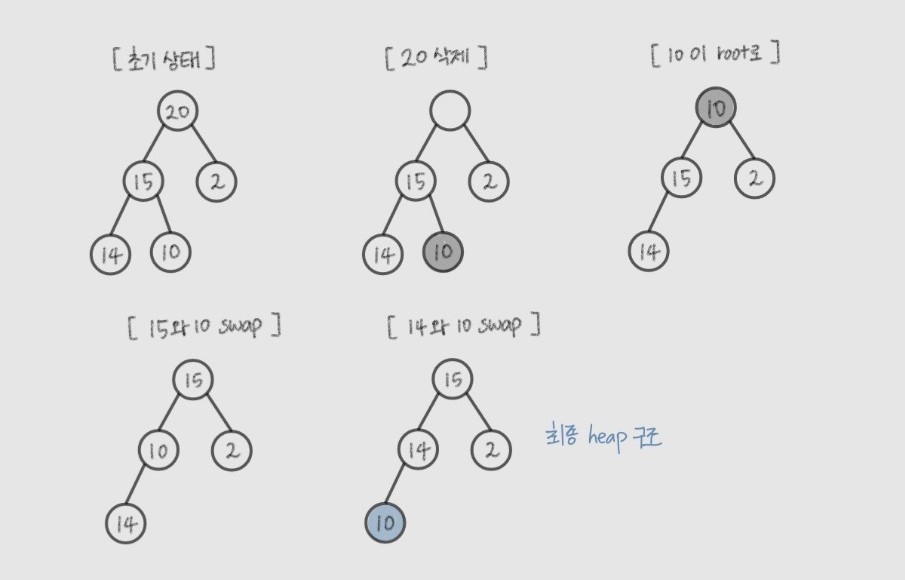
• 삭제 위치 : 항상 root
• 삭제 후 complete binary tree가 되도록 재조정
  • 가장 마지막에 있는 node를 root에 놓고, 자식 node들을 비교하면서 아래 방향으로 scanning

큐(Queue), 우선순위 큐 (priority queue)

• 힙을 이용해서 우선순위 큐를 구현할 수 있다! 큐, 우선순위 큐

파이썬 heapq 모듈

• list를 min heap으로 사용할 수 있도록 도와주는 모듈
• min heap을 사용하면…
  • 원소들이 항상 정렬된 상태로 삽입·삭제
  • index 0 = 가장 작은 수 = root node = 1st priority = 가장 먼저 삭제
• 내부 구현

  • 직계후손보다 크기가 작거나 같다.

      heap[k] <= heap[2*k+1] and heap[k] <= heap[2*k+2]
    

• 사용 예시

    # 내장모듈 임포트
    import heapq
      
    # heapq에 사용할 리스트 생성
    heap = []
      
    # min heap에 원소 삽입
    heapq.heappush(heap,4)
    heapq.heappush(heap,1)
    heapq.heappush(heap,7)
    heapq.heappush(heap,3)
    # 이후 [1,3,7,4]로 정렬되어 있다.
      
    # min heap에서 원소 삭제
    # 참고로 원소 하나 삭제할 때마다 정렬한다!
    heapq.heappop(heap)
    # 이후 [3,4,7]로 정렬되어 있다.
      
    # 기존 리스트를 min heap으로 변환
    heap2 = [4,1,7,3,8,5]
    heapq.heapify(heap2)
    # 이후 [1,3,5,4,8,7]로 정렬되어 있다.