[ 데이터구조 ] Tree

트리

• directed(위→아래) acyclic graph!
  • 뭔 말인가 싶은가요?

트리 용어

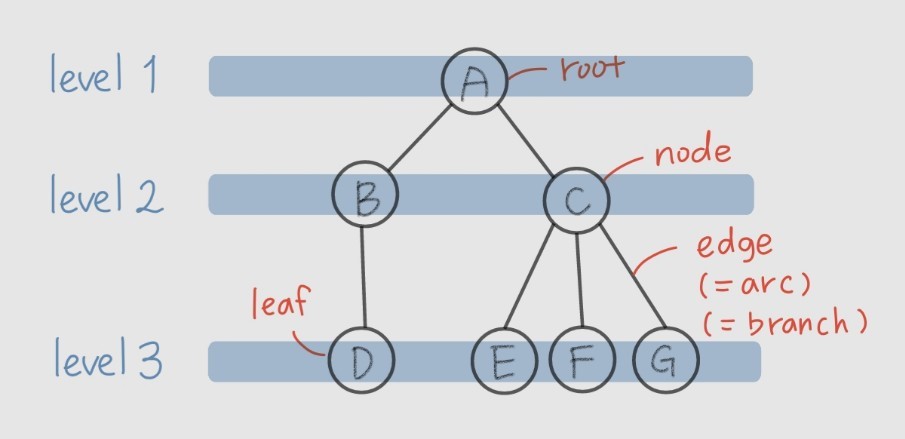
• 노드의 degree : branch 개수
• depth : tree의 최대 level → 현재 예시는 depth = 3
• 사실상 트리의 각 노드에 올 수 있는 edge의 개수는 무한 개다.
  • edge 개수를 (최대) 2개로 고정시키자! → binary tree!

이진트리

• 각 node의 edge의 개수가 최대 2개인 트리
• depth K의 최대 노드 개수 : $2^K-1 (K≥1)$
  e.g.) depth=3인 경우 최대 노드는 $2^3-1=7$개이다.

이진트리의 종류

full binary tree

• 최대 노드 개수 $2^K-1 (K≥1)$를 가진 이진트리

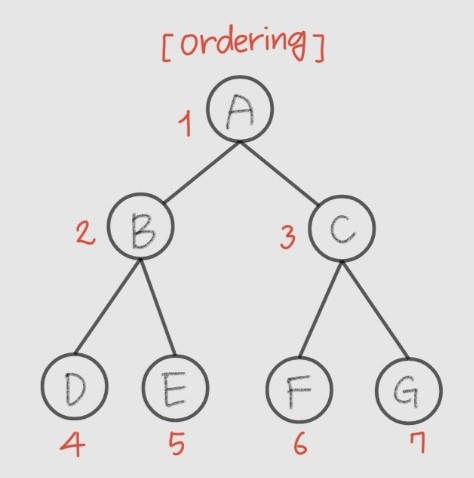
complete binary tree

• full binary tree의 ordering을 따르는 이진트리

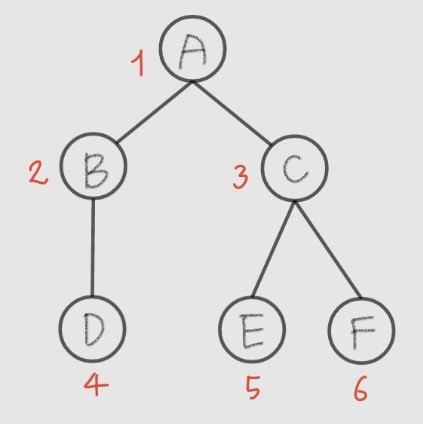
skewed tree

• 한쪽으로 치우친 트리 → TERRIBLE!

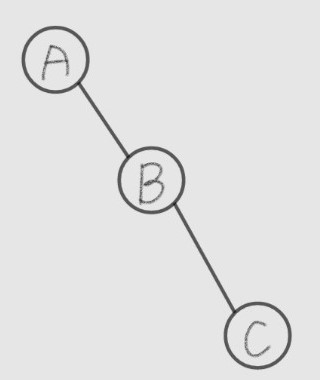
이진트리 순회

순회(traversal)

• 모든 node 한 번씩만 방문
• 순회 시 할 수 있는 동작들
  • left edge로 간다. (L; left edge)
  • 현재 node를 방문한다. (V; visit)
  • right edge로 간다. (R; right edge)

순회 종류

단 L과 R이 있을 때 L→R 순서로 간다고 가정한다.

중위순회 (In-order traversal) LVR (left → visit →right)

전위순회 (Pre-order traversal) VLR(visit → left → right)

후위순회 (Post-order traversal) LRV(left → right → visit)

순회 예시

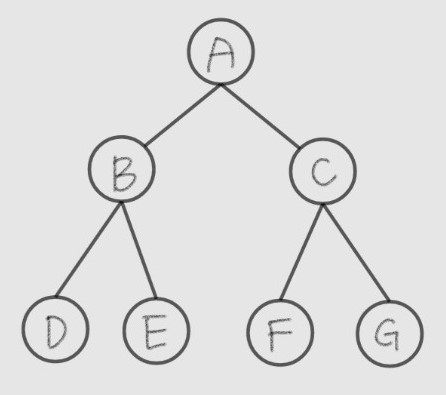
순회 종류	방문 순서
중위 (LVR)	D B E A F C G
후위 (LRV)	D E B F G C A
전위 (VLR)	A B D E C F G

이진탐색트리(BST; Binary Search Tree)

이진탐색 (이분탐색; Binary Search)

이진탐색트리

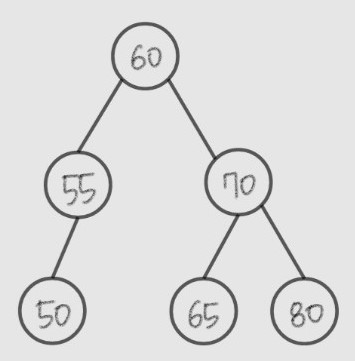
• 모든 노드들이 서로 다른 값을 가진다.
• left subtree에 있는 값들은 현재 노드의 값보다 작다.
• right subtree에 있는 값들은 현재 노드의 값보다 크다.
• complete binary tree는 아니다.

이진탐색트리의 탐색법

def BST(tree, key):  # tree : 현재의 수를 가리키는 포인터, key : 찾는 수
        while tree:  # 이진탐색트리가 비어있지 않다면 실행
                if key == tree: # 현재 찾는 수를 가리키고 있다면
                        return tree
                elif key < tree:  # 현재 가리키는 수가 찾는 수보다 크다면
                        tree = left_child # 왼쪽 child로 이동 (작은 수 찾아야 한다.)
                else:  # 현재 가리키는 수가 찾는 수보다 작다면
                        tree = right_child # 오른쪽 child로 이동 (큰 수 찾아야 한다.)