[ 딥러닝 ] Convolutional Neural Networks

Convolutional Neural Networks의 특징

• feed-forward network
  • convolution
  • pooling
  • non-linearity
• supervised learning
• training convolutional filters by back-propagating error

Convolution

\[g=f*h\]

$g=f*h$ where $\begin{cases} g(x,y)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x+u,y+v)h(u,v)dudv \ \,
g(x,y)= \sum_{u,v} f(x+u,y+v)h(u,v)\end{cases}$

Convolutional Layer

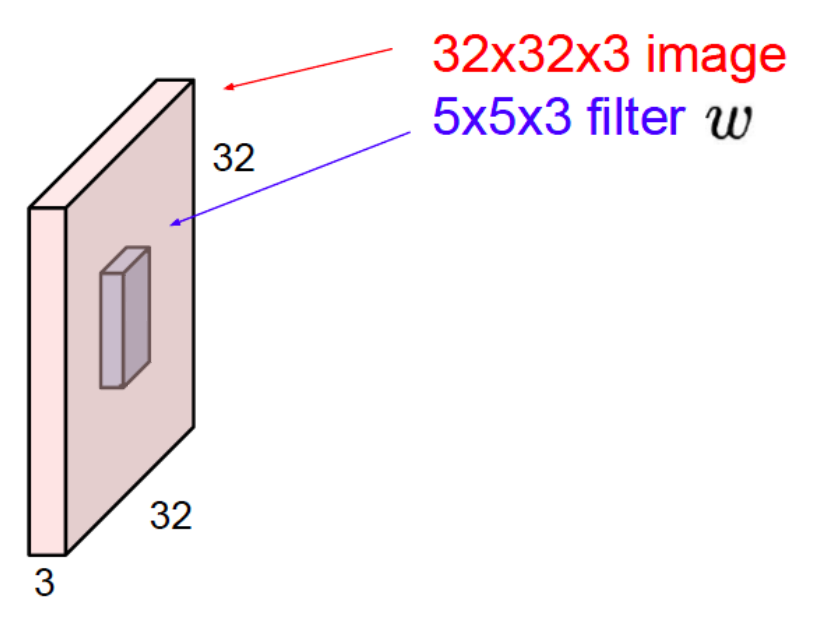
• input 크기 : $(H,W,C)$
• kernel 크기 : $(K_H, K_W, K_C)$
• output 크기 : $(O_H,O_W,O_C)$

• stride : 기본적으로 1

• kernel을 거친 출력 size?
  • stride가 1인 경우
  \[O_H = H - K_H + 1 ,\,\,\, O_W = W - K_W + 1 \\ \, \\ ∴ output = input-kernel+1\]
  • stride가 1보다 큰 경우
  \[O_H = \frac{(H - K_H)}{(stride)} + 1 ,\,\,\, O_W = \frac{(W - K_W)}{(stride)} + 1\]
• kernel size?

  • stride가 1인 경우

    \[K_H = H-O_H+1 ,\,\,\, K_W = W-O_W+1 \\ \, \\ ∴ kernel = input-output+1\]

  • stride가 1보다 큰 경우

  \[K_H = H-\{(stride)*(O_H-1)\}\]
• 사실상 kernel은 각 픽셀에 weight를 곱해주는 역할이다.
  • 위의 예시에선 총 75개의 parameter(=5Χ5Χ3 weights)가 존재하는 상황이다.

• 채널이 여러 개인 경우 2D Convolution을 채널 수만큼 적용하는 것이다.

  

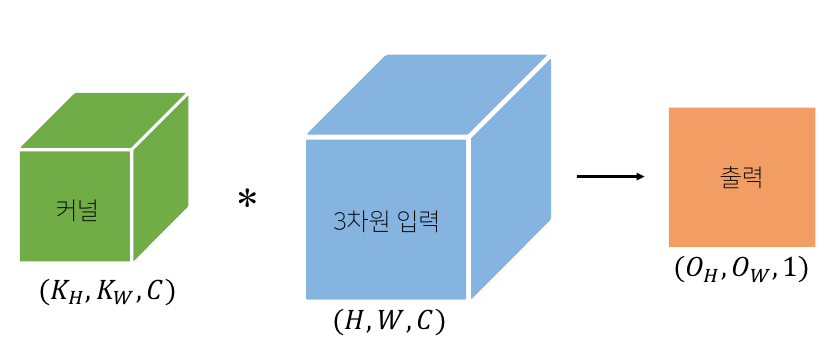
  • kernel을 $O_C$개 만큼 적용하면 출력의 channel도 $O_C$이다.

    

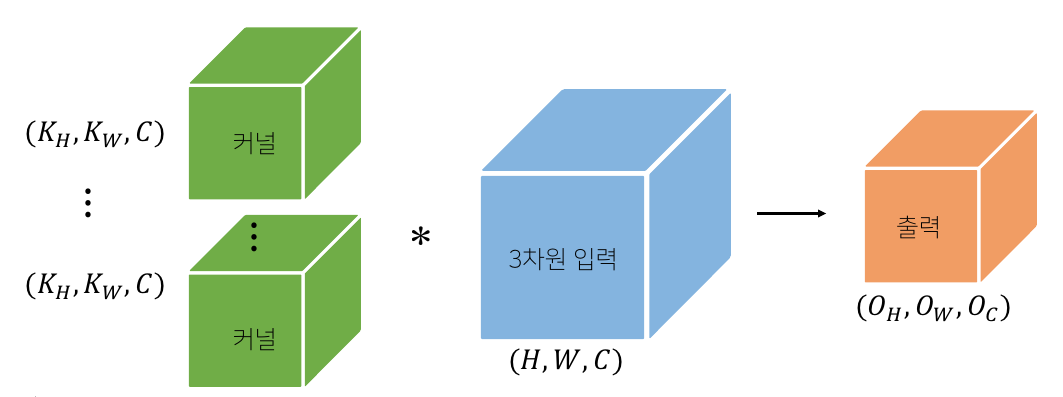
• ConvNet은 convolutional layer들의 모임이다.

  

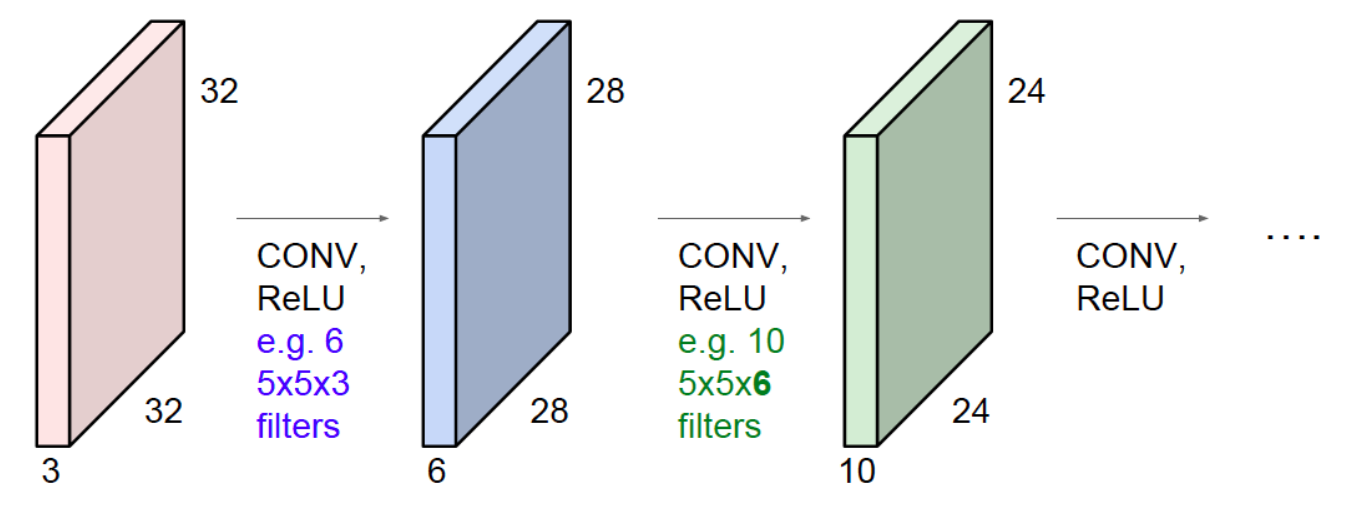
  • 매번 convolution한 결과를 activation function (여기서는 ReLU)에 넣는다.
  • activation function 없으면 linear transformation한 것과 다를 게 없다.

stride

• downsampling 역할
• 위의 상황에서 stride 3이라면 output의 size?
  • $\frac{32-5}{3}+1=10$이므로 $output:(10,10,1)$

padding

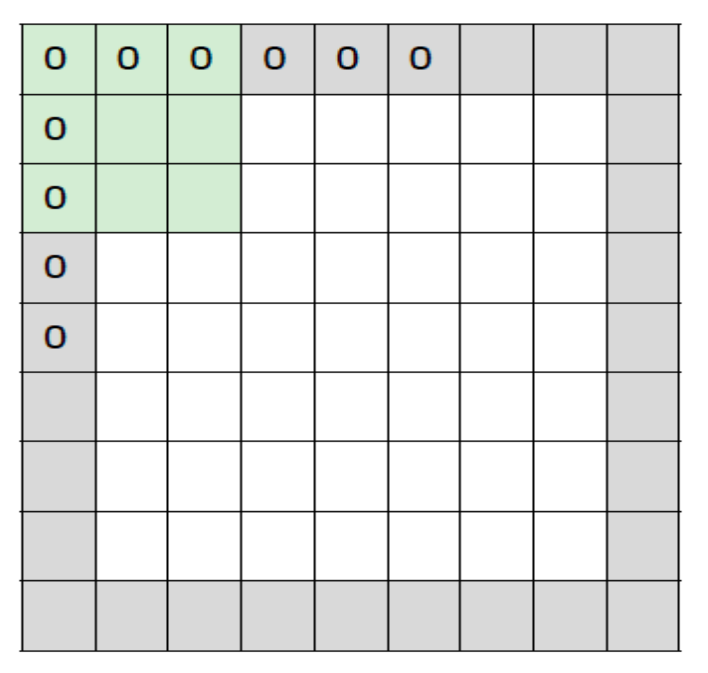
• input size와 동일하게 output이 나올 수 있도록 0으로 테두리를 채우는 것
• kernel size가 $(F,F)$라 하면, $(F-1)/2$ 만큼의 zero-padding을 하면 된다.
  • $kernel=(3,3)$이면 $pad=1$ (예시의 그림)
  • $kernel=(5,5)$이면 $pad=2$

Pooling Layer

• feature map의 size를 줄이는 역할을 한다.

max pooling

• kernel 내에 들어오는 픽셀 값 중 최대값을 선택한다.

average pooling

• kernel 내에 들어오는 픽셀 값의 평균을 취한다.

Fully-Connected Layer

• each is connected to an entire region in the input
• no parameter sharing

MLP와 CNN의 차이점

• parameter 수가 감소했다.
• weight sharing