[ 딥러닝 ] Multi-Layer Perceptron

Neural Networks

• affine transformation을 쌓는 방식이다.
  • 즉, nonlinear transformation

  • [참고] affine transformation vs. linear transformation

    affine transformation = linear transformation + translation (평행이동)

Linear Neural Networks

Linear Model

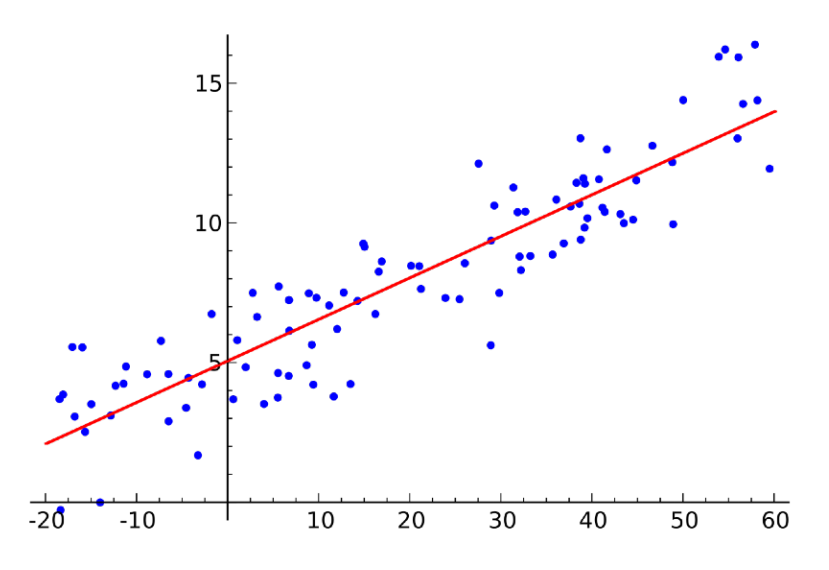
• data : $\mathcal{D} = {(x_i,y_i)}^N_{i=1}$

• model : $\hat{y} = wx + b$

• loss : $\frac{1}{N}\sum_{i=1}^N (y_i-\hat{y_i})^2$

• gradient of loss :

  \[\begin{align*} \frac{\partial loss}{\partial w} & = \frac{\partial}{\partial w}\frac{1}{N}\sum_{i=1}^N (y_i-\hat{y_i})^2 \\ & = \frac{\partial}{\partial w}\frac{1}{N}\sum_{i=1}^N (y_i-wx_i-b)^2 \\ & = -\frac{1}{N}\sum_{i=1}^N -2(y_i - wx_i -b)x_i \end{align*}\]

• 선형대수적 표현

  

  \[\mathbf{y}=\mathbf{W}^T \mathbf{x}+\mathbf{b}\]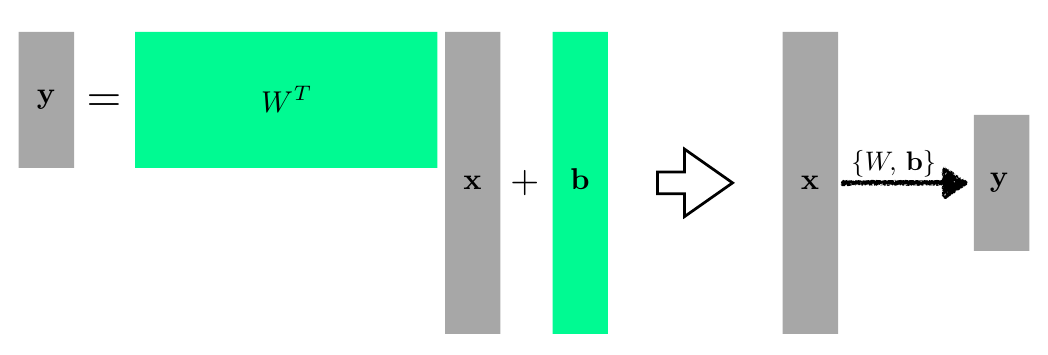

  • 층을 여러 개 쌓는다면…

    

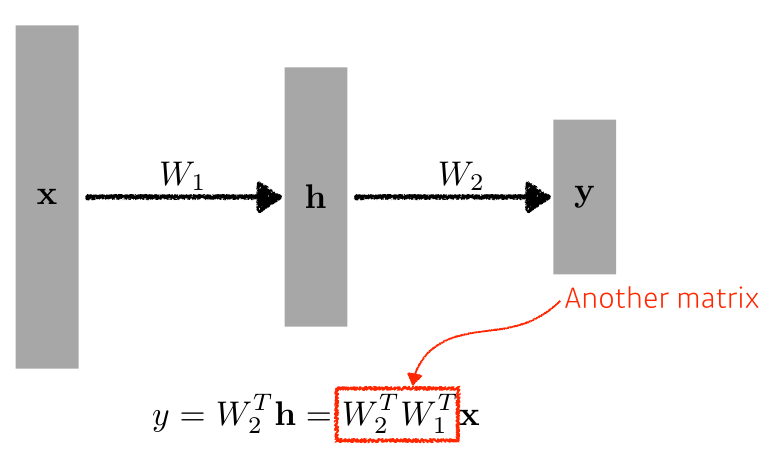
    • 여러 층을 지나도 weight 부분은 결국 matrix multiplication을 하면 새로운 ‘하나’의 weight가 되므로 linear해진다.

Nonlinear Transform

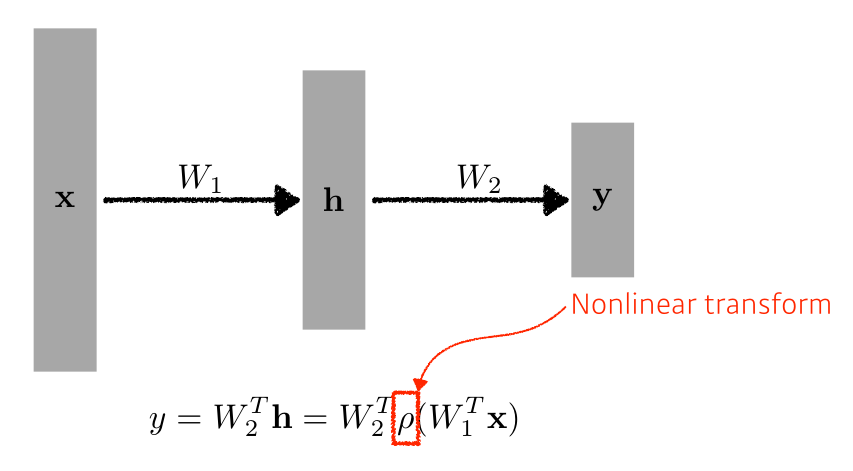
• nonlinearity를 추가하기 위해 activation function을 사용한다!

Activation Function

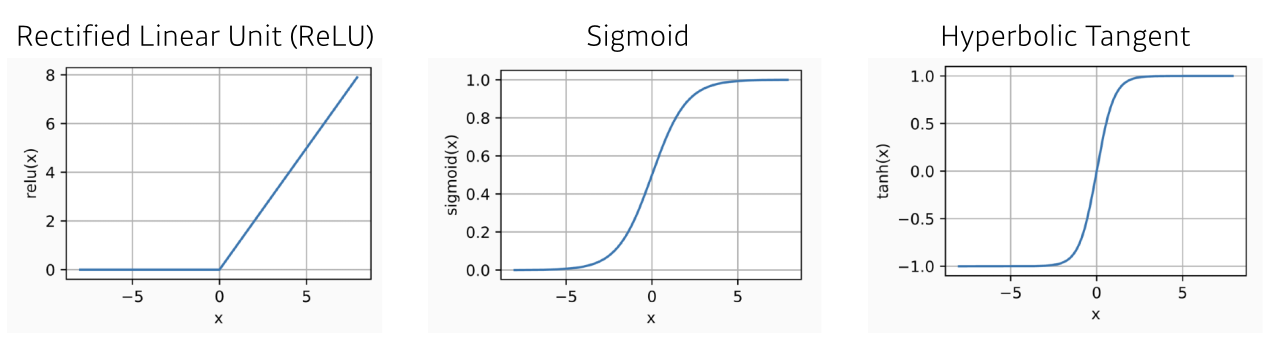
MLP (multi-layer perceptron)

• 간단한 구조

  

  \[y=W^T_3 \mathbf{h}_2=W^T_3 \rho(W^T_2 \mathbf{h}_1)=W^T_3 \rho(W^T_2 \rho(W^T_1 \mathbf{x}))\]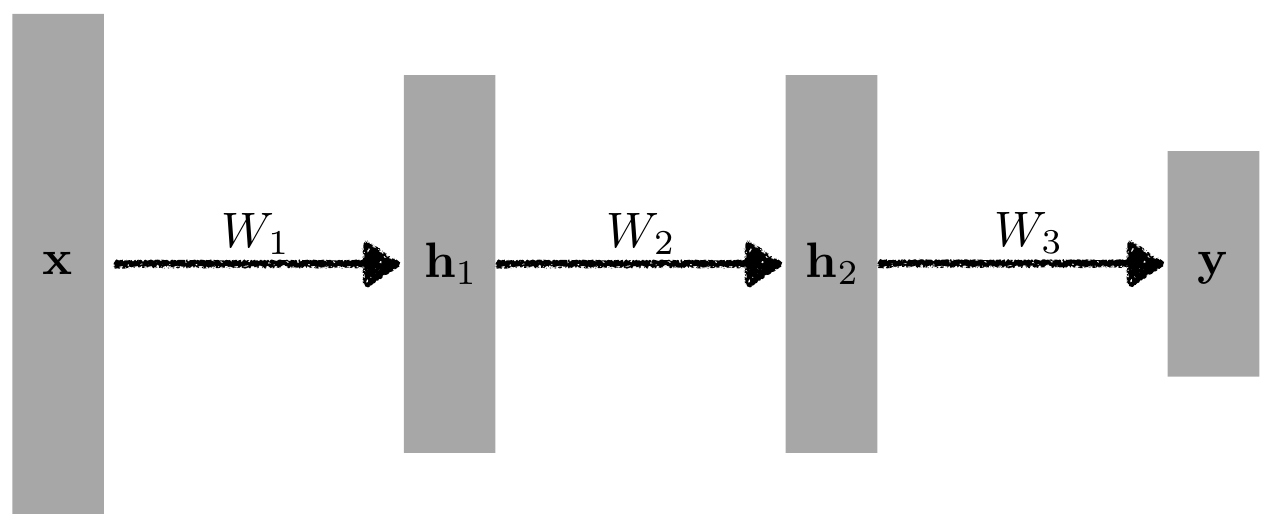

• loss function

  • Regression Task

    \[MSE=\frac{1}{N} \sum_{i=1}^N \sum_{d=1}^D (y_i^{(d)}-\hat{y}_i^{(d)})^2\]

  • Classification Task

    \[CE=-\frac{1}{N} \sum_{i=1}^N \sum_{d=1}^D y_i^{(d)} log \;\hat{y}_i^{(d)}\]

  • Probabilistic Task

    \[MLE=\frac{1}{N} \sum_{i=1}^N \sum_{d=1}^D log \mathcal{N}(y_i^{(d)};\hat{y_i}^{(d)},1)\]