[ 딥러닝 ] Optimization - part 2

Gradient Descent Methods

stochastic gradient descent

• data sample 하나에 대해 gradient descent 시행

mini-batch gradient descent

• 작은 데이터 덩어리에 대해 gradient descent 시행

(total) batch gradient descent

• 데이터 전체에 대해 한 번에 gradient descent 시행

Gradient Descent

\[W_{t+1} ← W_t-\eta g_t\]

• ‘적절한’ learning rate를 설정하는 것이 쉽지 않다!
  • 너무 작으면 오래 걸린다.
  • 너무 크면 minimum을 지나칠 수 있다.

Momentum

\[a_{t+1} ← \beta a_t + g_t \,\,\,(\beta : momentum) \\ \, \\ W_{t+1} ← W_t-\eta a_{t+1}\]

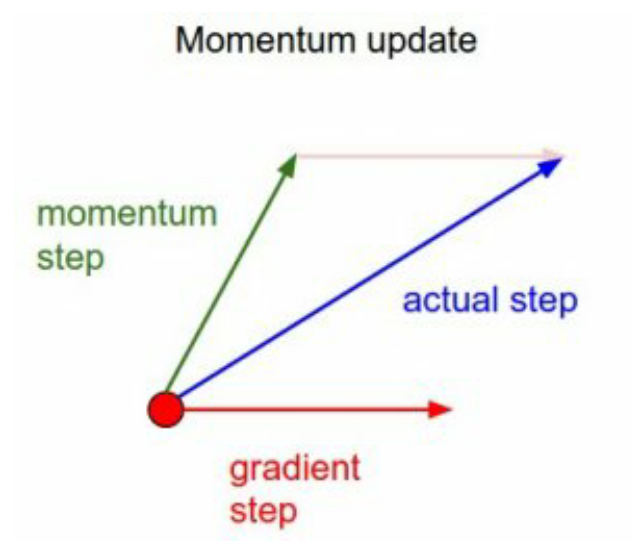
• 현재 gradient의 방향과는 별개로, 과거에 이동했던 방향으로 일정 정도를 추가 이동하자.
• $\beta$가 클수록 이전 속도(gradient 방향)를 더 따른다.
• $\beta$는 보통 0.9로 사용한다.

Nesterov Accelerated Gradient

\[a_{t+1} ← \beta a_t + \nabla \mathcal{L}(W_t- \eta \beta a_t) \,\,\, (\nabla \mathcal{L}(W_t- \eta \beta a_t) : lookahead\,\, gradient) \\ \, \\ W_{t+1} ← W_t-\eta a_{t+1}\]

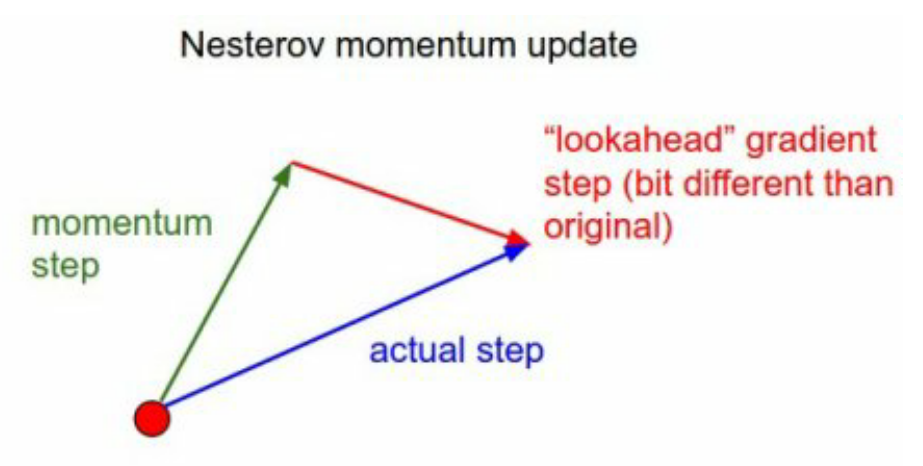
• momentum step만큼 가보고 그 곳에서의 gradient를 추가하게 된다.
• 일반 Momentum보다 빠르게 minimum에 converge할 수 있다.

Adagrad

\[W_{t+1} ← W_t-\frac{\eta}{\sqrt{G_t+\epsilon}} g_t \\ \, \\ G_t = G_{t-1}+g_t^2 = \sum_{i=0}^t(\frac{\partial}{\partial w(i)} cost(w(i)))^2\]

• adaptive gradient
• parameter의 변화량을 본다.
  • 변화량이 큰 parameter는 적게 변화시킨다.
  • 변화량이 작은 parameter는 크게 변화시킨다.
• $G_t$ : sum of gradient squares (이제껏 gradient가 얼마나 변했는가)
• 한계점 : 학습이 길어질수록 $G_t$가 커지므로 $\frac{\eta}{\sqrt{G_t+\epsilon}}$은 작아지게 되어 parameter 업데이트가 중단될 수 있다.

RMSprop

\[W_{t+1} ← W_t-\frac{\eta}{\sqrt{G_t+\epsilon}} g_t \\ \, \\ G_t = \gamma G_{t-1} + (1-\gamma) \, g_t^2\]

• Adagrad에 EMA 개념을 더해서 $G_t$가 무한히 커지는 것을 방지하는 방법

• EMA (exponential moving average; 지수 이동 평균)?

  \[x_k = \alpha p_k + (1-\alpha )x_{k-1} \,\,\,\, (\alpha=\frac{2}{N+1}) \\ \, \\ x_k = \alpha \sum_{t=0}^{N-1} (1-\alpha)^t \,p_{k-t} + (1-\alpha)^N x_{k-N}\]
  • 최근 값을 더 잘 반영하기 위해 최근 값과 이전 값에 각각 가중치를 주어 계산하는 방법
  • 1주기가 지날 때마다 ‘1-α’라는 가중치가 이전 값에 곱해지므로 시간이 지날수록 영향력이 줄어드는 효과를 볼 수 있다.

Adadelta

\[W_{t+1} ← W_t-\frac{\sqrt{H_{t-1}+\epsilon}}{\sqrt{G_t+\epsilon}} g_t \\ \, \\ G_t = \gamma G_{t-1} + (1-\gamma) \, g_t^2 \\ \, \\ H_t = \gamma H_{t-1}+(1-\gamma)(\Delta W_t)^2\]

• $H_t$ : EMA of difference squares (이제껏 weight가 얼마나 변했는가)

Adam

\[W_{t+1} ← W_t-\frac{\eta}{\sqrt{v_t+\epsilon}} \frac{\sqrt{1-\beta^t_2}}{1-\beta_1^t} \, m_t \\ \, \\ v_t = \beta_2 v_{t-1} + (1-\beta_2) \, g_t^2 \\ \, \\ m_t = \beta_1 m_{t=1} + (1-\beta_1)g_t\]

• Adaptive Moment Estimation
• EMA of gradient squares $v_t$ + EMA of momentum $m_t$
• gradient square의 크기에 따라서 adaptive하게 learning해서 바꾸는 것 + 이전의 gradient 정보에 해당하는 momentum
• 가장 많이 사용하는 optimizer이다.