[ 딥러닝 ] Recurrent Neural Networks - part 1

Sequential Model

Sequence Data

• 이전의 데이터와 현재 데이터가 연쇄적으로 관련있는 데이터
  • 소리, 문자열, 주가, 시계열
• iid를 위배하는 경우가 많아 순서 변경 혹은 데이터 손실 발생 시 확률분포도 변경된다.
  • iid (independent and identically distribution, 독립항등분포) : 각각의 random variable이 독립이고, 같은 확률분포를 가진다.

Naive Sequential Model

\[\begin{align*} P(X_1,...,X_t) & = P(X_t|X_{t-1},...,X_1)P(X_{t-1},..,X_1) \\ \, \\ & = P(X_t|X_{t-1},...,X_1)P(X_{t-1}|X_{t-2},...,X_1)P(X_{t-2},...,X_1) \\ \, \\ & = \prod_{s=1}^t P(X_s|X_{s-1},...,X_1) \end{align*}\]

• 현재’까지의’ 데이터가 발생할 확률을 구하려면 각 시간 데이터에 대한 조건부확률을 ‘모두’ 알아야 한다. 하지만 조건부에 들어가는 데이터 길이가 가변적이다.

Autoregressive (AR) Model

\[P(X_t|X_{t-1},...,X_\tau)\]

• 현실적으로 모든 과거 정보가 필요한 것이 아니므로 일부 시점 전까지의 데이터에 대해서만 구하는 것으로 근사한다.
• 일정 시점 전 $\tau$ 까지만 보는 모델

(1st order) Markov Model

\[\begin{align*} P(X_T,...,X_1) & = P(X_T|X_{T-1})P(X_{T-1}|X_{T-2})...P(X_2|X_1)P(X_1) \\ \, \\ & = \prod_{t=1}^T P(X_t|X_{t-1}) \end{align*}\]

• $\tau=1$인 경우의 모델 (즉, 바로 이전 시점의 데이터까지만 고려한다.)
• 1st order autoregressive model 이라고도 한다.

Latent Autoregressive Model

\[\begin{align*} & \hat{x_t} = P(X_t|h_t) \\ \, \\ & h_t = f_{W}(h_{t-1},X_{t-1}) \end{align*}\]

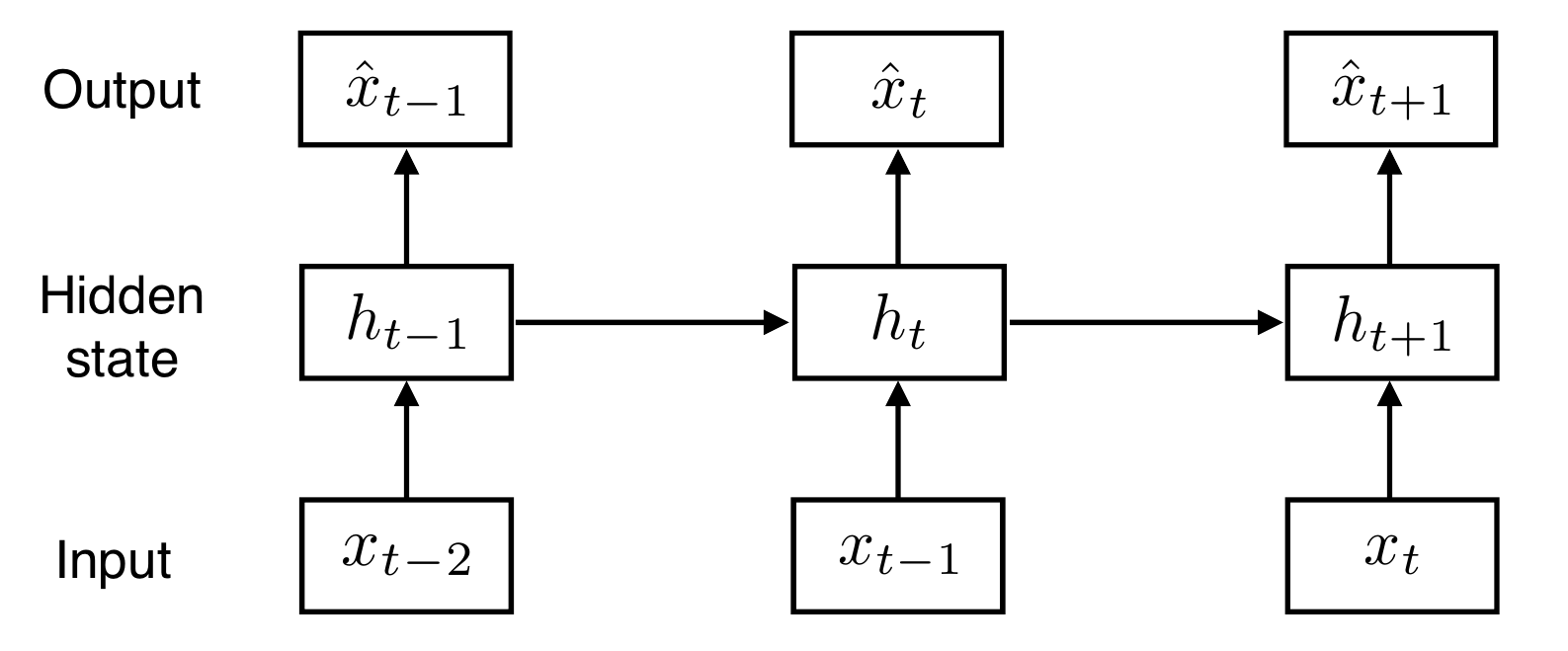
• AR, Markov model과 달리 이전의 데이터를 다 사용하는 모델
• 바로 이전 빼고 나머지 전부를 새로운 잠재변수로 인코딩해서 사용
• 이전 시점의 hidden state와 현재 input을 활용한다.
  • hidden state $h_t$
    • hidden state = latent vector
    • 과거의 정보를 요약한 것
    • (이번 time step에 대한) 출력이자 (다음 time step에 대한) 입력

Recurrent Neural Network

[NLP] Language Model

• 문장 혹은 단어열에 대한 확률분포 할당하는 모델
  • 이전 단어들이 주어졌을 때 다음 단어를 예측하도록 하는 모델
• 종류
  • 통계기반 : N-gram
  • 신경망 기반 : RNN

vanilla RNN

\[\begin{align*} & y_t = h_tW_{hy} \\ \, \\ & h_t = tanh(W_{hh}^T h_{t-1}+W_{hy}x_t) \end{align*}\]

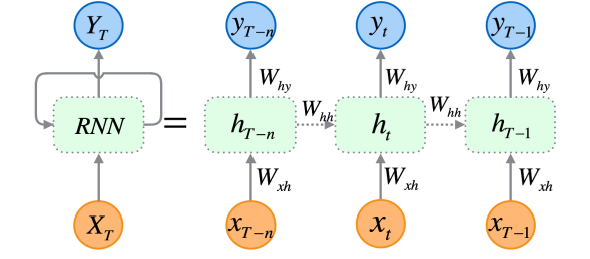
• MLP와 유사하며 latent vector를 Neural Net으로 반복 사용
• 사실상 입력이 굉장히 많은 FC layer
• 무작위 길이 → 고정된 길이(∵softmax)의 벡터
• [NLP] 입력 주기 이전까지의 과정 : word embedding
• cell에서 되돌아가는 화살표로 표현한 이유
  • latent vector (function)의 형태가 모든 time step에서 동일하므로
• parameter sharing
  • 모든 시점에서 parameter가 동일하게 적용된다.
    • parameter?
      • input을 hidden으로 보내는 $W_{xh}$
      • 이전 hidden에서 현재 hidden으로 보내는 $W_{hh}$
      • hidden에서 out으로 보내는 $W_{hy}$