[ Basic AI Math ] Bayes Statistics
Updated:
조건부 확률
- 사건 A와 B가 동시에 발생할 확률 (with 조건부 확률)
-
조건부 확률을 이용해서 정보를 갱신할 수 있다.
-
\[P(B|A) = \frac{P(A∩B)}{P(A)}=P(B)\frac{P(A|B)}{P(A)}\]A라는 새로운 정보가 주어졌을 때 $P(B)$로부터 $P(B A)$를 계산하는 방법을 제공한다.
-
Bayes’ Theorem
\[P(B|A) = P(B)\frac{P(A|B)}{P(A)}\]- 새로운 정보를 토대로 어떤 사건이 발생했다는 주장에 대한 신뢰도를 갱신해 나가는 방법
- 확률 : 주장에 대한 신뢰도
- 용어
-
$P(B A)$ : 사후확률 (posterior) - 새로운 사건이 발생했을 때 기존 사건이 발생할 확률 -
$P(B)$ : 사전확률 (prior) - 기존의 사건이 발생할 확률
-
$P(A B)$ : 가능도(likelihood) - 기존의 사건이 발생했을 때 새로운 사건이 발생할 확률 - $P(A)$ : evidence - 새로운 사건이 발생할 확률
-
-
예제)
-
풀이
-
조건부 확률의 시각화
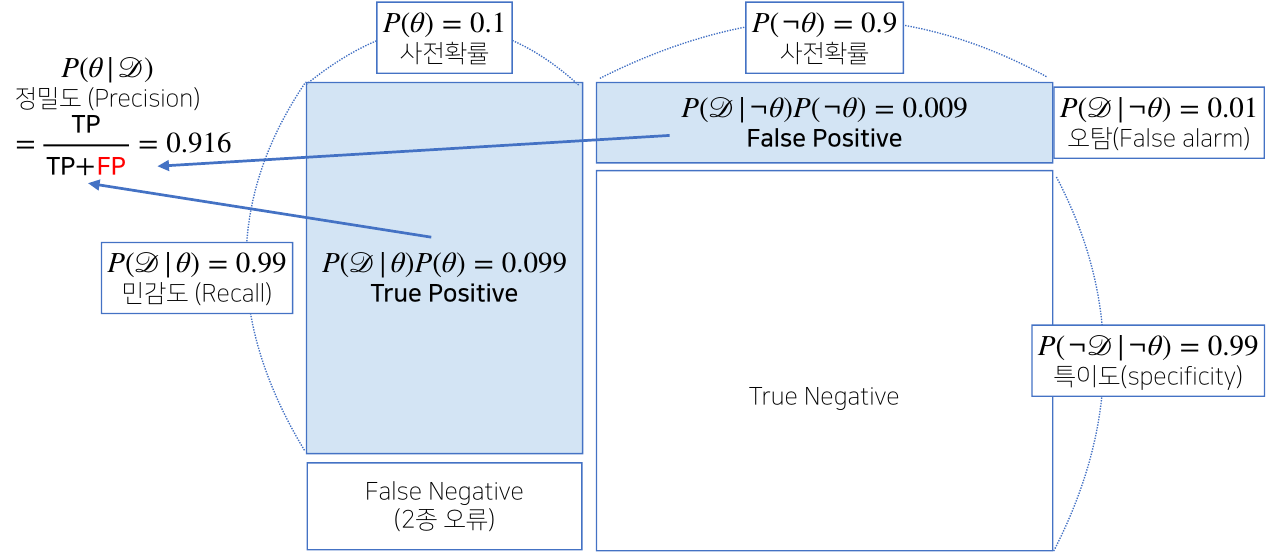
-
$P(\mathscr{D} \theta)$ : 기존의 사건이 발생했을 때 새로운 사건이 발생했다는 것에 대한 신뢰도 - likelihood = recall
-
$P(\theta \mathscr{D})$ : 새로운 사건이 발생했을 때 기존 사건이 발생했다는 것에 대한 신뢰도 - posterier probability = precision
Bayes’ thm.을 이용한 정보의 갱신
- 새로운 데이터가 들어왔을 때 사후확률을 사전확률로 사용하여 갱신된 사후확률 계산 가능
-
e.g.) 앞서 COVID-19 양성 판정을 받은 사람(→사전확률!)이 두번째 검진에서 양성판정을 받았을 때, 진짜 COVID-19에 걸렸을 확률?
\[P(B|A)=0.1*\frac{0.99}{0.189}≈0.524 \\ \; \\ \begin{align*} P(A^*) &= P(A^*|B)P(B)+P(A^*|\neg B)P(\neg B) \\&=P(A|B)P(B|A)+P(A|\neg B)\cdot \neg P(B|A) \\&= 0.99*0.524+0.1*0.476≈0.566 \end{align*} \\ \; \\ P(B|A^*)=0.524*\frac{0.99}{0.566}≈0.917\]
조건부 확률 → 인과관계?
조건부 확률 vs. 인과관계
- 조건부 확률 : 인과관계(causality)를 추론할 때 함부로 쓰지 않는다!
- 조건부 확률이 곧 인과관계가 되지는 않는다!
인과관계 (Causality)
- 데이터 분포 변화에 robust한 예측 모형을 만들 때 필요하다.
- 새로운 데이터가 들어온 경우
- 조건부 확률 기반 : 시나리오에 따른 변동이 크다.
- 인과관계 기반 : 시나리오에 따른 변동이 작다.
- 새로운 데이터가 들어온 경우
- 중첩요인(confounding factor) 제거 후 원인에 해당하는 변수만의 인과관계를 계산해야 한다.
- 중첩요인 : 여러 사건의 원인이 되는 사건
-
예제)
| | 전체 | 작은 결석 | 큰 결석 | | — | — | — | — | | treatment a | 78% (273/350) | 93% (81/87) | 73% (192/263) | | treatment b | 83% (289/350) | 87% (234/270) | 69% (55/80) |
- 치료법
- treatment a : 개복 수술
- treatment b : 수술 기법
- 치료법 a, b에 따른 완치율 차이?
- Simpson’s Paradox
- 여러 그룹의 자료를 합했을 때의 결과와 각 그룹을 구분했을 때의 결과가 다른 경우
- 현 상황에서의 중첩요인 : 신장결석 크기
- 조정 효과(intervention)
- 신장 결석 크기를 고려하지 않고 치료법에 따른 완치율을 비교하는 것
-
치료법을 a로 고정했을 때 전반적인 완치율
\[\begin{align*} P^{ℭ_a}(R=1) &=\sum_{z∈\{0,1\}}P^{ℭ}(R=1|T=a,Z=z)P^{ℭ}(Z=z) \\ \; \\ &= \frac{81}{87}*\frac{(87+270)}{700}+\frac{192}{263}*\frac{(263+80)}{700}≈0.8325 \end{align*}\]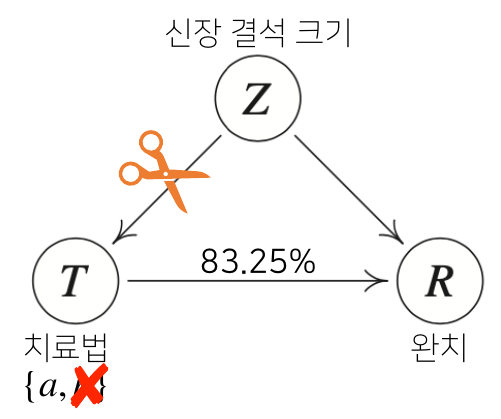
-
치료법을 b로 고정했을 때 전반적인 완치율
\[\begin{align*} P^{ℭ_b}(R=1) &= \sum_{z∈\{0,1\}}P^{ℭ}(R=1|T=b,Z=z)P^{ℭ}(Z=z) \\ \; \\ &= \frac{234}{270}*\frac{(87+270)}{700}+\frac{55}{80}*\frac{(263+80)}{700}≈0.7789 \end{align*}\]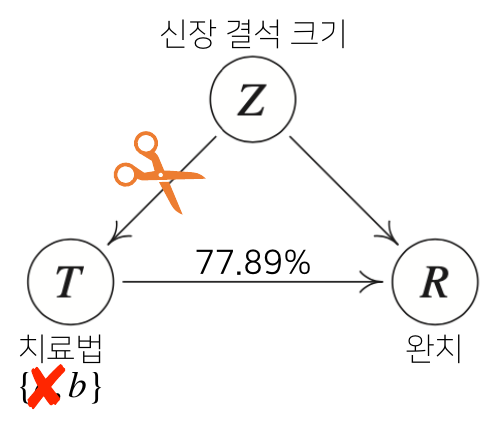
- 치료법
