[ Basic AI Math ] Vector

벡터

• 숫자 배열
• 다차원 공간에서의 한 점
• 원점으로부터의 상대적 위치

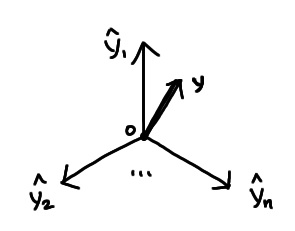
• 벡터 $Y = [y_1,y_2,…,y_n]$라 하면 우측과 같이 표현할 수 있다.

  

벡터의 연산

스칼라곱

길이만 변화된다.

덧셈, 뺄셈

• 상대적 위치 이동
• 원래는 동일한 size여야 연산 가능하다!
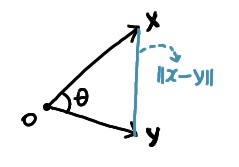
• 뺄셈 : 두 벡터 사이의 거리

벡터의 norm

• 원점에서부터의 거리 (n차원으로 개념 확장)

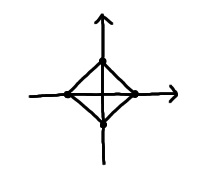
• $L_1$ norm (Manhattan Distance)

  

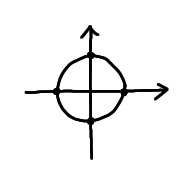
• $L_2$ norm (Euclidean Distance)

  

두 벡터 사이의 각도 (in $L_2$ norm)

제 2 코사인 법칙

\[cosθ = \frac{||x||^2 \ + ||y||^2 \ - ||x-y||^2 }{2\ ||x||\ ||y||}\]

벡터의 내적

\[cosθ = \frac{<x,y>}{\|x\| \; \|y\|} \\ \; \\ <x,y>=\sum x_iy_i\]